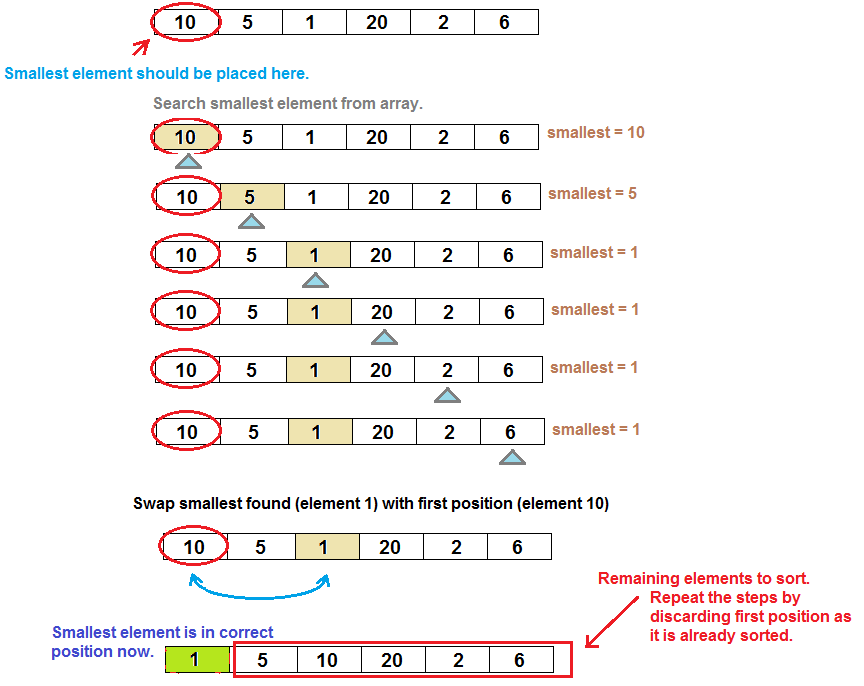
Selection Sort

✅ Selection Sort Code O(n²)

def selection_sort(arr):
    for i in range(len(arr)):  # Iterate through each index where the next smallest element should go
        min = i  # Assume current index holds the minimum
        for inner in range(i+1, len(arr)):  # Find the smallest in the remaining array
            if arr[inner] < arr[min]:  
                min = inner  
        arr[i], arr[min] = arr[min], arr[i]  # Swap found minimum with current position
    return arr

📝 Quick Review for Fast Recall

• ✅ Set left-most element as smallest → Scan from left-most element+1 to n-1 → Find the smallest in the scan → Swap left-most with scanned-smallest → Repeat
• ✅ O(n²) complexity → Bad for large inputs
• ✅ O(1) space → In-place sorting
• ✅ Minimizes swaps → Useful for memory-constrained environments
• ✅ Not stable → Relative order of equal elements may change
• ✅ Use Case? When minimizing swaps is critical, like in limited memory write scenarios. Otherwise, go for better algorithms.
• ✅ Better alternatives? QuickSort (O(n log n)), MergeSort (O(n log n))

⏳ Time Complexity & Number of Operations (Selection Sort)

• ✅ Best Case (Already Sorted): O(n²) → Still iterates fully but minimal swaps
• ✅ Worst Case (Reverse Sorted): O(n²) → Maximum comparisons and swaps
• ✅ Average Case (Random Order): O(n²) → Consistently inefficient for large datasets
• ✅ Space: O(1) → In-place sorting
• ✅ Total comparisons: (n² - n) / 2
• ✅ Total swaps: O(n)

⚠️ Traps & Things to Watch Out For

• Misplacing swap logic: Swap should happen after finding the minimum, not inside the inner loop.
• Wrong index comparison: Always compare arr[j] < arr[min], not arr[i] < arr[min].
• Inefficiency for large inputs: Not optimal for big datasets—mention better alternatives like QuickSort or MergeSort.
• Avoid using "min" as a variable name (Python has a built-in min() function). Rename to min_ind if necessary.
• Selection Sort vs. Bubble Sort?
  • Selection sort minimizes swaps but has the same time complexity.
  • Bubble sort is stable, but Selection Sort is not.