✅ Insertion Sort Code O(n²)
def insertion_sort(arr):
n = len(arr)
for i in range(1, n):
key = arr[i] # Store the value to be inserted
j = i - 1
# Shift elements of arr[0..i-1] that are greater than key
while j >= 0 and arr[j] > key:
arr[j + 1] = arr[j]
j -= 1
# Insert the stored value at the correct position
arr[j + 1] = key
return arr
📝 Quick Review for Fast Recall
- ✅ Comparison-based sorting algorithm
- ✅ Stable: Does not change the relative order of elements with equal values
- ✅ In-place: Uses O(1) extra space
- ✅ Efficient for small or nearly sorted datasets
- ✅ Not efficient for large datasets
⏳ Time Complexity & Number of Operations
- ✅ Best Case (Already Sorted): O(n) → Only compares, no shifting
- ✅ Worst Case (Reverse Sorted): O(n²) → Each element inserted at the beginning
- ✅ Average Case (Random Order): O(n²) → Expected number of swaps = O(n² / 4)
- ✅ Total possible pairs in an array: n * (n – 1) / 2
- ✅ Worst-case inversions (reverse sorted): n * (n – 1) / 2
- ✅ Best-case inversions (already sorted): 0
- ✅ Average-case inversions (random order): n * (n – 1) / 4
⚠️ Traps & Things to Watch Out For
- ✅ Off-by-one errors: Be careful with boundary conditions in loops
- ✅ Unoptimized comparisons: If detecting a sorted array, stop early to reduce complexity
- ✅ Confusion between i and j: Ensure j shifts elements and i marks the next pivot
- ✅ Inefficient for large inputs: Avoid for n > 1000; use QuickSort/MergeSort instead
📌 Steps
- ✅ Start iterating from index 1: Treat the first element as sorted
- ✅ Set pivot element (key = A[i]): This is the element to be placed in the correct position
- ✅ Initialize comparison pointer j = i - 1: Start from the last sorted element
- ✅ Shift elements if necessary: While A[j] > key, shift A[j] to A[j+1] and decrement j
- ✅ Insert key at the correct position: Key is placed at A[j+1] ensuring left side remains sorted
- ✅ Repeat for all elements: Continue until the entire array is sorted
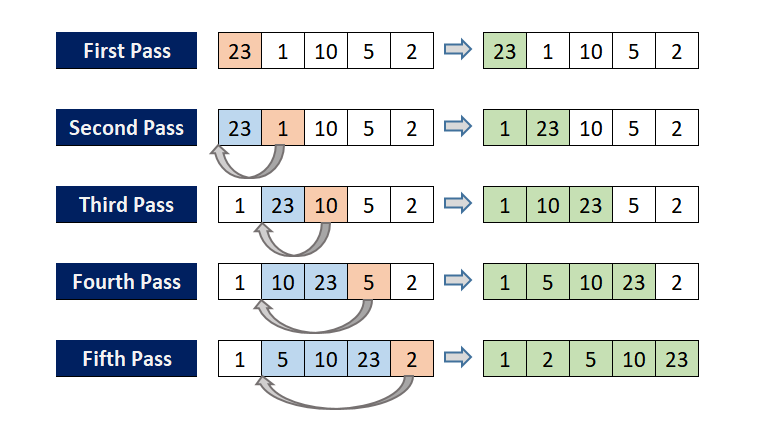
Insertion Sort (key at ith,jth,sorted, unsorted)