Insertion Sort

✅ Insertion Sort Code O(n²)

def insertion_sort(arr):
    n = len(arr)
    
    for i in range(1, n):
        key = arr[i]  # Store the value to be inserted
        j = i - 1
        
        # Shift elements of arr[0..i-1] that are greater than key
        while j >= 0 and arr[j] > key:
            arr[j + 1] = arr[j]
            j -= 1
        
        # Insert the stored value at the correct position
        arr[j + 1] = key
    
    return arr

📝 Quick Review for Fast Recall

• ✅ Comparison-based sorting algorithm
• ✅ Stable: Does not change the relative order of elements with equal values
• ✅ In-place: Uses O(1) extra space
• ✅ Efficient for small or nearly sorted datasets
• ✅ Not efficient for large datasets

⏳ Time Complexity & Number of Operations

• ✅ Best Case (Already Sorted): O(n) → Only compares, no shifting
• ✅ Worst Case (Reverse Sorted): O(n²) → Each element inserted at the beginning
• ✅ Average Case (Random Order): O(n²) → Expected number of swaps = O(n² / 4)
• ✅ Total possible pairs in an array: n * (n – 1) / 2
• ✅ Worst-case inversions (reverse sorted): n * (n – 1) / 2
• ✅ Best-case inversions (already sorted): 0
• ✅ Average-case inversions (random order): n * (n – 1) / 4

⚠️ Traps & Things to Watch Out For

• ✅ Off-by-one errors: Be careful with boundary conditions in loops
• ✅ Unoptimized comparisons: If detecting a sorted array, stop early to reduce complexity
• ✅ Confusion between i and j: Ensure j shifts elements and i marks the next pivot
• ✅ Inefficient for large inputs: Avoid for n > 1000; use QuickSort/MergeSort instead

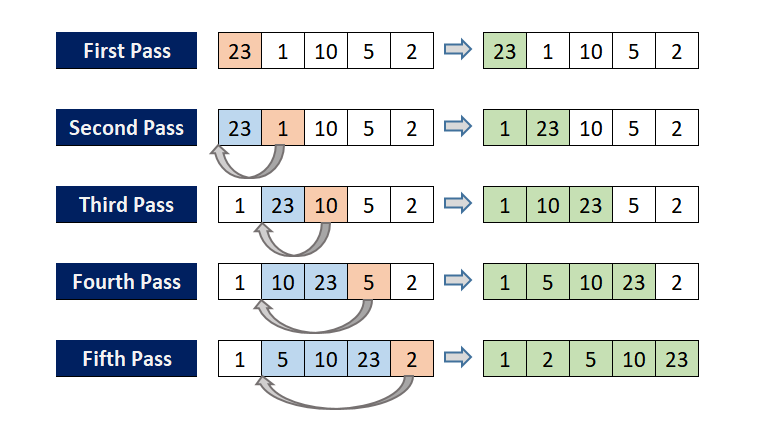
📌 Steps

• ✅ Start iterating from index 1: Treat the first element as sorted
• ✅ Set pivot element (key = A[i]): This is the element to be placed in the correct position
• ✅ Initialize comparison pointer j = i - 1: Start from the last sorted element
• ✅ Shift elements if necessary: While A[j] > key, shift A[j] to A[j+1] and decrement j
• ✅ Insert key at the correct position: Key is placed at A[j+1] ensuring left side remains sorted
• ✅ Repeat for all elements: Continue until the entire array is sorted