Bubble Sort

✅ Bubble Sort Code O(n²)

def bubble_sort(arr):
    for start in range(len(arr)):
        for i in range(len(arr)-1, start, -1):
            if arr[i - 1] > arr[i]:
                (arr[i - 1], arr[i]) = (arr[i], arr[i - 1])

📝 Quick Review for Fast Recall

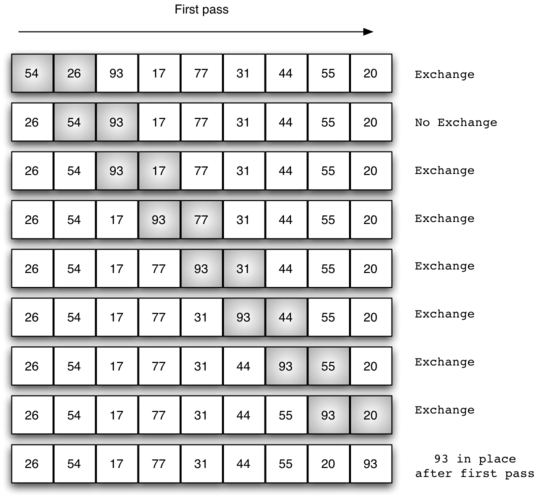
• ✅ Compare adjacent elements → Swap if out of order → Repeat until sorted
• ✅ O(n²) complexity → Inefficient for large datasets
• ✅ O(1) space → In-place sorting
• ✅ Stable → Preserves relative order of equal elements
• ✅ Use Case? Simple implementation, useful for small datasets or teaching purposes.
• ✅ Better alternatives? QuickSort (O(n log n)), MergeSort (O(n log n))

⏳ Time Complexity & Number of Operations (Bubble Sort)

• ✅ Best Case (Already Sorted): O(n) → Single pass without swaps
• ✅ Worst Case (Reverse Sorted): O(n²) → Maximum swaps and comparisons
• ✅ Average Case (Random Order): O(n²) → Performance remains poor
• ✅ Space: O(1) → In-place sorting
• ✅ Total comparisons: (n² - n) / 2
• ✅ Total swaps: O(n²) in worst case

⚠️ Traps & Things to Watch Out For

• Unnecessary comparisons: Optimized versions stop early if no swaps occur.
• Inefficiency: Not practical for large inputs—consider QuickSort or MergeSort.
• Confusion with other sorts: Bubble Sort is stable, while Selection Sort is not.